Nous avons vu diverses structures de filtres.

Nous cherchons ici à calculer les coefficients d'un filtre pour répondre à une spécification donnée.

Cette spécification peut être, dans certains cas (filtrage adapté à un signal), donnée sous forme d'une réponse impulsionnelle. Si cette réponse est finie, on a vu que les échantillons de cette réponse sont les coefficients d'un filtre R.I.F. Il n'y a donc aucune difficulté.

La spécification peut être donnée sous forme d'un gain en fréquence. Il n'y a alors généralement pas de filtre d'ordre fini qui réponde exactement à cette spécification. Il est nécessaire d'accepter un écart à la réponse idéale souhaitée. Cet écart pourrait être spécifié comme un écart quadratique maximum. Cela n'est généralement pas satisfaisant. On préférera donner des bornes du gain dans diverses bandes de fréquences : le gabarit.

Partons de la réponse idéale du filtre. C'est une porte si nous prenons l'exemple de la synthèse d'un filtre passe-bas.

La réponse impulsionnelle idéale en est sa transformée de Fourier . On obtient ici une fonction de support infini. Le filtre idéal n'est pas réalisable. Il est donc nécessaire d'approcher cette réponse infinie par une réponse finie. Le plus simple est de tronquer cette réponse idéale et de ne garder que la partie centrale qui comprend les valeurs les plus grandes. Cette opération peut se modéliser par le produit de la réponse idéale par une fonction porte temporelle.

Le gain en fréquence obtenu est alors la convolution du gain idéal par la transformée de Fourrier de la porte.

On constate alors l'apparition d'ondulations importantes autour de la réponse en fréquence idéale. On peut réduire l'étendue de ces ondulations en augmentant la longueur de la réponse impulsionnelle conservée, mais pas l'amplitude de ces ondulations. Pour réduire ces ondulations, il faut "arrondir les angles" de la porte qui effectue la troncation. On remplace la porte par une fonction à variation plus lente : une fenêtre d'apodisation.

On constate que la diminution des oscillations se fait au détriment de la raideur du filtre. Le choix de la fonction d'apodisation sera le résultat d'un compromis.

Il existe quelques fonctions classiques utilisées comme fonction d'apodisation. On peut les caractériser par deux paramètres. Le premier est la largeur du pic principal de leur transformée de Fourier, qui se traduira par la largeur de la bande de transition au voisinage de la fréquence de coupure. Le deuxième est l'amplitude des lobes de cette transformée, que l'on exprimera, en décibel, comme l'atténuation correspondant au premier lobe du gain d'un filtre passe-bas réalisé avec cette fenêtre.

On part d'une forme idéale de réponse en fréquence. On spécifie le filtre d'une part par la largeur de transition entre les bandes passantes et atténuées et d'autre part par l'atténuation en bande atténuée. On choisit la forme de la fenêtre d'apodisation qui permet d'atteindre l'atténuation désirée. On calcule ensuite la durée de la réponse impulsionnelle et donc le nombre de points de la réponse discrète. On termine par une vérification du gain en fréquence. Si les fréquences de coupures du filtre sont suffisamment éloignées, on obtient le résultat souhaité. Sinon, il les oscillations autour de deux transitions peuvent se combiner et donner des atténuations trop faibles. Il faudra alors itérer en changeant un paramètre.

Attention à prendre un grand nombre de points pour la définition du gain idéal : le gain est une fonction d'une variable continue qu'il faut approximer par un grand nombre de points. Attention au piège de le transformée de Fourier Discrète : si on définit le gain par un trop faible nombre de points, le gain du filtre, qui est une fonction continue de la fréquence, peut prendre entre ces points des valeurs très différentes des valeurs spécifiées. Or une simple TFD ne montre que les points qui sont justes.

Pour des signaux courts, le filtrage peut être fait par multiplication dans le domaine des fréquences. Il est alors tentant de réaliser un filtrage de type passe-bande par une simple multiplication de la TFD par une porte. On a alors l'illusion d'un filtrage parfait. On constate qu'il n'en est rien si on interpole en fréquence le résultat obtenu. Il convient d'une part d'utiliser l'une des méthodes de synthèse précédentes pour calculer la réponse impulsionnelle, puis d'en faire le TFD et d'autre part de prendre garde à la périodicité du filtrage par TFD. On pourra éventuellement se contenter d'une méthode simple : "arrondir" la porte par un point intermédiaire de valeur 0,5. Cela revient à réaliser une apodisation de Hanning, mais il subsiste une erreur due à la circularité.

Tous les logiciels de traitement du signal disposent d'une implémentation d'un algorithme de synthèse utilisant une technique d'optimisation numérique. Avantage : paramétrage indépendant des bandes de fréquence. En particulier, les tolérances peuvent être différentes entre les bandes passantes et les bandes atténuées. On obtient donc, pour un filtre de gabarit donné, une réponse impulsionnelle plus courte, dont moins coûteuse en calcul.

On sait que le gain en fréquence d'un filtre est l'expression de sa transformée en z sur le cercle unité. La synthèse d'un filtre récursif revient donc à trouver les coefficients d'une équation aux différences dont la transformée en z a les valeurs désirée sur le cercle unité.(ou les pôles d'une fraction rationnelle en "z" qui réponde à la même condition.). Ce problème n'en en général pas de solution exacte.

Il se trouve que l'on connaît quelques modèles de filtres continus de type passe bande que l'on sait adapter pour obtenir les qualités de raideur et d'atténuation souhaités. La méthode de synthèse la plus employée est une transposition de ces filtres continus en filtres discrets

Soit et respectivement l'entrée et la sortie d'un filtre continu.

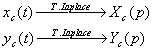
Ce filtre continu est décrit par sa fonction de transfert en "p".

Le gain en fréquence du filtre est l'expression de cette fonction de transfert sur l'axe imaginaire

De plus, on sait que ce filtre est stable si ses pôles sont situé à gauche de l'axe imaginaire.

Soit et respectivement l'entrée et la sortie d'un filtre discret.

Ce filtre discret est décrit par sa fonction de transfert en "z"

Le gain en fréquence du filtre est l'expression de cette fonction de transfert sur le cercle unité :

De plus, on sait que ce filtre est stable si ses pôles sont situés à l'intérieur du cercle unité.

Le but de la transformation est transformer l'expression en une expression de tel sorte que le gain du filtre discret soit le même que celui du filtre continu. Il faudrait pour cela que, dans la transformation, l'axe imaginaire se transforme en le cercle unité. Or le premier et de support infini et le second de support fini. Il ne sera donc pas possible de répondre à ce problème de façon complètement satisfaisante.

De plus, pour conserver la stabilité, il faut que la partie gauche de l'axe imaginaire se retrouve à l'intérieur du cercle unité.

Nous avons vu que l'on peut obtenir un filtre équivalent à un filtre continu ("cf. Filtrage Hybride") en prenant pour réponse impulsionnelle du filtre discret l'échantillonnée de la réponse impulsionnelle continue, à condition de respecter la condition de Shannon. C'est ce que l'on fait toujours pour les filtres R.I.F.

Il parait donc logique de faire de même pour les filtres R.I.I.

Soit un filtre continu de réponse impulsionnelle .

La réponse impulsionnelle du filtre discret est

Supposons que la fonction de transfert du filtre continue (qui est la transformée de Laplace de sa réponse impulsionnelle) soit décomposable en somme de termes du premier ordre. Cela qui signifie qu'il n'y a que des pôles simples .

Chacun des termes du premier ordre a une RI exponentielle :

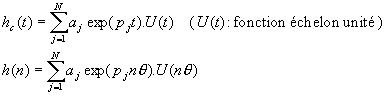
Calculons la transformée en Z, en sommant à partir de 0 en raison de la causalité de la RI

ce qui s'écrit :

Les pôles du filtre continu sont transformés en des pôles dans le filtre discret. On peut voir que les pôles du filtre continu situés à gauche de l'axe imaginaire sont transformés en des pôles situés à l'intérieur du cercle unité. La stabilité est donc bien conservée.

Par contre, le gain en fréquence du filtre discret n'est pas exactement celui du filtre continu. En effet, la réponse en fréquence d'un filtre n'est pas rigoureusement bornée, même pour un filtre passe bas : cette réponse tend asymptotiquement vers 0 à l'infini. L'échantillonnage ne respecte donc strictement jamais la condition de Shannon ; il y aura toujours un repliement. Ce repliement sera souvent de faible amplitude, mais dégradera la qualité de l'atténuation du filtre aux hautes fréquences.

Cette méthode est basée sur un équivalent numérique de l'intégrateur analogique utilisant la méthode d'approximation de l'intégrale continue par la méthode des trapèzes.

Soit l'intégrale de la fonction .

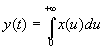
Dans le domaine de Laplace :

La fonction de transfert de l'intégrateur est donc :

On cherche à obtenir une approximation de cette intégrale en utilisant les échantillons de .

En l'approxime par l'aire des trapèzes formés en joignant les échantillons entre eux.

Dans le domaine de la transformée en Z :

La fonction de transfert en Z de l'intégrateur discret réalisé avec l'approximation des trapèzes est donc :

Pour transformer un filtre continu, défini par sa fonction de transfert en , en un filtre discret défini par sa fonction de transfert en , en utilisant cette approximation, il suffit d'effectuer la transformation suivante :

Cette transformation est nommée "transformation bilinéaire".

Etudions comment se transforme l'axe imaginaire

En observant que l'expression obtenue est le quotient de deux termes conjugués :

L'axe imaginaire se transforme en le cercle unité. On peut vérifier que les points situés à gauche de l'axe imaginaire se transforment en des points situés à l'intérieur du cercle : la stabilité des filtres est donc bien conservée.

Comparons les gains en fréquence du filtre continu et du filtre numérique obtenu.

Le gain du filtre continu est obtenu en décrivant l'axe imaginaire. On retrouve bien ces valeurs de gain

sur le cercle unitaire aux points .

D'autre part, le gain du filtre numérique est obtenu en décrivant le cercle unitaire, aux points

Les deux gains seront donc égaux pour

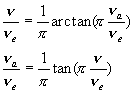
Le filtre numérique à donc les mêmes valeurs de gain que le filtre continu, mais pour des fréquences différentes. Il se produit une distorsion de l'axe des fréquences.

Pour des filtres de type passe-bande, ce défaut peut être compensé en effectuant une pré-distortion inverse.

Méthode de synthèse :

• Spécification du filtre numérique : fréquences de coupures
• Prédistortion : calcul des fréquences de coupure du filtre analogique :
• Calcul de la fonction de transfert du filtre continu ayant ces fréquences de coupure.
• Transformation bilinéaire

On caractérise ces modèles par la forme du modèle de type passe-bas normalisé.

• Filtre de Butterworth : gain monotone en fonction de la fréquence (sans oscillation).
• Filtres de Tchebychef : Plus raide. Oscillation en bande passante, monotone en bande atténuée.
• Filtre elliptique ou de Cauer. C'est celui qui répond le mieux à la spécification d'un gabarit. Ondulation en bande passante et affaiblie.

On sait ensuite passer d'un modèle normalisé à un filtre de coupure donnée, puis d'un passe-bas à un passe-haut ou à un passe bande.

Le critère déterminant sera souvent la phase. Si l'on veut imposer une phase (une phase linéaire en particulier), le RIF s'impose. Sinon, le plus faible nombre de coefficients des filtres R.I.I. sera préféré. Il faudra tout de même regarder si le nombre de coefficients plus grand du R.I.F. n'est pas compensé par l'apport de la TFD rapide ou par le filtrage multi-cadence.