Application de la TFD à l'analyse spectrale
Signaux certains de durée limitée
On a montré que la TFD du signal échantillonné donnait presque exactement des échantillons de la TF continue du signal continu. Rappelons que l'échantillonnage nécessite que la bande spectrale du signal soit limitée, ce qui n'est pas rigoureusement possible pour un signal à durée limitée. Il y aura donc toujours un léger repliement, que l'on minimisera par une fréquence d'échantillonnage![]() suffisamment grande.
suffisamment grande.
Quelle est la résolution de l'analyse ? Elle est donnée par le pas d'échantillonnage en fréquence ![]() .
.
Or ![]()

Figure 7 : Signal et sa transformée. En raison de la périodicité, les fréquences positives apparaissent sur la droite. Par permutation circulaire, on peut obtenir une visualisation plus physique.
Pour obtenir une résolution plus fine, la seule possibilité est d'augmenter N (sans changer ![]() !). Cela se fait en prolongeant le signal par des valeurs nulles. Bien entendu, cela n'apporte pas d'information. Celle opération ne fait qu'une interpolation de la TF, pour obtenir une courbe plus facile à interpréter à l'œil, ou pour permettre de mesurer la position d'un pic plus précisément.
!). Cela se fait en prolongeant le signal par des valeurs nulles. Bien entendu, cela n'apporte pas d'information. Celle opération ne fait qu'une interpolation de la TF, pour obtenir une courbe plus facile à interpréter à l'œil, ou pour permettre de mesurer la position d'un pic plus précisément.
|
Ajout de zéro en tempsó Interpolation en fréquence |
Remarque : on peut utiliser une technique similaire, pour interpoler un signal temporel
|
Ajout de zéro en fréquence ó Interpolation en temps |
Signaux certains de durée infinie
La TFD ne s'applique qu'aux signaux de durée finie (qui sont considérés comme une période d'un signal périodique). Un signal infini est nécessairement tronqué, ce qui introduit des erreurs.
Remarque : ce problème n'est pas spécifique au traitement numérique. On ne le connaît pas en électronique analogique parce qu'on ne sait pas faire l'opération de TF. Par contre, il est connu en optique.
Soit ![]() le signal tronqué. On peut le modéliser par le produit du signal
le signal tronqué. On peut le modéliser par le produit du signal ![]() par une porte
par une porte ![]() de durée
de durée ![]() .
.
![]()
Le transformée de Fourier est donc convoluée par la TF de cette porte
![]()
Observons les effets de cette convolution sur un signal sinusoïdal. Il apparaît sur ![]() des sinus cardinaux à la place des Dirac de
des sinus cardinaux à la place des Dirac de ![]() .Les passages par zéro de ces sinus cardinaux sont espacés de
.Les passages par zéro de ces sinus cardinaux sont espacés de ![]()
Or la TFD donne l'échantillonnage de ![]() , avec un pas d'échantillonnage
, avec un pas d'échantillonnage
![]()
qui est exactement égal à la demi pseudo période du sinus cardinal.
On voit que si la période du signal est un sous multiple exact de la durée d'analyse, le résultat parait "bon" : on obtient un Dirac.
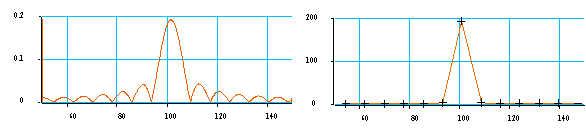
Par contre dans les autres cas, il apparaît des "pieds" aux pics.
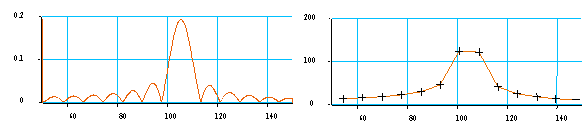
Pour minimiser cet effet, on peut remplacer la porte par une fonction plus "douce", dont la TF présente des lobes moins importants. Cette fonction est appelée fonction d'apodisation. Cela se fait au prix de la résolution : les pics sont élargis. Il faudra donc dans le choix de cette fonction de pondération, régler un compromis entre, d'un part l'amplitude des lobes secondaires, qui peuvent cacher des pics de faible amplitude au voisinage d'un pic de forte amplitude, et d'autre part la largeur des pics, qui peuvent empêcher de séparer deux pics fréquences très proches.
L'échantillonnage en fréquence induit également un autre défaut : si aucun échantillon ne tombe sur le sommet du lobe principal, la valeur du maximum d'un pic de la TFD est plus faible que la valeur de ce pic sur la TF continue. L'élargissement de ce pic créé par l'apodisation à sur ce point un effet bénéfique : le pic étant moins pointu l'amplitude des points situés à son voisinage se rapprochent de l'amplitude du maximum. Certains analyseurs proposent une fonction "flat-top" dont le sommet de la TF et suffisamment plat pour rendre cette erreur acceptable, mais cela se fait aux prix d'une diminution extrême de la sélectivité. Il sera préférable, si cela est possible d'interpoler le TFD par ajout de zéro en temps comme cela est expliqué ci-dessus.
Signaux aléatoires (introduction)
On sait qu'il est nécessaire d'effectuer des moyennes pour estimer un paramètre statistique. On sait également que, grâce à la propriété d'ergodisme, on peut remplacer la moyenne statistique (sur des réalisations différentes ) par un moyennage temporel (sur des échantillons successifs). Donc, pour réaliser l'analyse spectrale, plutôt que de prendre une seule tranche du signal comme précédemment, on peut prendre plusieurs tranches successives.
Supposons que l'on dispose d'un enregistrement numérique de ![]() échantillons d'une réalisation d'un signal aléatoire. On divise cet enregistrement en
échantillons d'une réalisation d'un signal aléatoire. On divise cet enregistrement en ![]() blocs de
blocs de ![]() échantillons.
échantillons.
![]()
On calcule les TFD ![]() de tous ces blocs.
de tous ces blocs.
La densité spectrale de puissance du signal est alors estimée par
![]()
Le pas d'échantillonnage du spectre estimé est donc
![]()
Pour obtenir une bonne résolution fréquentielle sur ce spectre, il est donc souhaitable de réduire ce pas, et donc d'augmenter la taille des blocs, ce qui revient à diminuer le nombre de blocs.
L'écart type de l'erreur statistique de l'estimation peut être calculée facilement en considérant que si les blocs sont disjoints, ils sont très peu corrélés. Les termes de la somme entrant dans le calcul du spectre sont alors des variables aléatoires indépendantes.
Donc
![]()
Pour obtenir une faible erreur statistique, il est donc souhaitable d'augmenter le nombre de blocs.
On constate qu'il est nécessaire de régler un compromis entre deux exigences contradictoires, la résolution en fréquence (la précision sur l'axe horizontal), et la qualité statistique (la précision sur l'axe vertical).
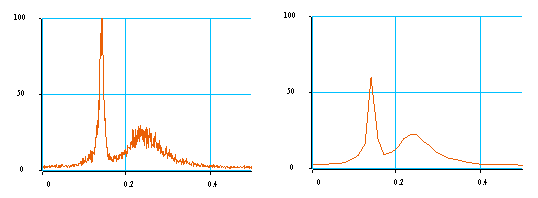
Figure 8 : Analyse d'un signal aléatoire de 32000 échantillons. A gauche, moyennage sur 32 blocs de 1024 valeurs. A droite, moyennage sur 512 blocs de 64 valeurs.
Mesure de densité d'énergie ou de puissance
Nous avons montré que la TFD donnait des échantillons exacts de la TF continue, à condition d'utiliser les formules introduites ci-dessus avec le facteur ![]() . Pour des signaux à spectre continu, il n'y a donc pas de problème. Si on calcule le module carré de la TFD (éventuellement moyennée dans le cas aléatoire) on obtient des valeurs correctes de la densité spectrale d'énergie (pour des signaux à durée finie). En divisant ce résultat (éventuellement moyennée dans le cas aléatoire) par la durée
. Pour des signaux à spectre continu, il n'y a donc pas de problème. Si on calcule le module carré de la TFD (éventuellement moyennée dans le cas aléatoire) on obtient des valeurs correctes de la densité spectrale d'énergie (pour des signaux à durée finie). En divisant ce résultat (éventuellement moyennée dans le cas aléatoire) par la durée ![]() de la tranche signal analysée, on obtient la densité spectrale de puissance (pour des signaux à durée infinie) en volts carrés par hertz. En général, on s'intéressera à des signaux réels. Dans ce cas, il sera plus physique de considérer que l'énergie dans une bande de fréquence est la somme de l'énergie dans cette bande plus l'énergie dans la bande symétrique en fréquence négative. Il faut donc affecter la mesure de densité d'énergie d'un facteur 2, ou l'amplidude de la TFD d'un facteur
de la tranche signal analysée, on obtient la densité spectrale de puissance (pour des signaux à durée infinie) en volts carrés par hertz. En général, on s'intéressera à des signaux réels. Dans ce cas, il sera plus physique de considérer que l'énergie dans une bande de fréquence est la somme de l'énergie dans cette bande plus l'énergie dans la bande symétrique en fréquence négative. Il faut donc affecter la mesure de densité d'énergie d'un facteur 2, ou l'amplidude de la TFD d'un facteur ![]() .
.
La mesure de la densité de puissance est faite à partir de l'énergie par blocs divisée par la durée (![]() )du bloc.
)du bloc.
Cela revient à un facteur supplémentaire de ![]() sur la TFD. Le coefficient de la TFD devient alors
sur la TFD. Le coefficient de la TFD devient alors
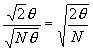
Remarquons que si l'on utilise une fonction d'apodisation, il faudra normaliser cette fonction de façon à ne pas modifier la puissance moyenne du signal. Il faut pour cela que l'intégrale du carré de la fonction discrète soit égale à ![]()
Cas particulier des signaux à spectre de raies.
Pour des signaux dont la TF présente des impulsions de Dirac, la notion de densité n'est plus utilisable, il est souhaitable d'obtenir les puissances de raies (en volts carrés) ou leur amplitude (en volts).
Soit un signal sinusoïdal
![]()
![]()
Comme on l'a vu précédemment, on en utilise seulement une partie. Cela revient à analyser ce signal multiplié par une porte ou par une fonction d'apodisation.
![]()
La transformée de Fourier en est :
![]() avec
avec ![]()
Soit ![]() la durée de la porte, les Diracs sont remplacés par des pics dont la hauteur est
la durée de la porte, les Diracs sont remplacés par des pics dont la hauteur est
![]()
![]() est la valeur à l'origine de la transformée de Fourier de la TF de la fonction d'apodisation. C'est donc plus simplement l'intégrale de la fonction d'apodisation. Si l'on n'apodise pas,
est la valeur à l'origine de la transformée de Fourier de la TF de la fonction d'apodisation. C'est donc plus simplement l'intégrale de la fonction d'apodisation. Si l'on n'apodise pas, ![]() est une fonction porte dont l'intégrale vaut
est une fonction porte dont l'intégrale vaut ![]() .
.
![]()
Pour mesurer la valeur de ce maximum par TFD, il faut calculer
![]()
Donc
![]()
On constate que le pas d'échantillonnage n'intervient pas dans cette mesure.
On préférera souvent calculer la valeur efficace ![]()
|
|
Si l'on apodise, on peut conserver cette formule à condition de normaliser la fonction d'apodisation de façon à ce que son intégrale (discrète) ait pour valeur ![]()
|
Pour faire mesurer la valeur efficace des raies d'un signal réel composé de fréquences pures, il faut normaliser la TFD par Pour mesurer une densité spectrale d'énergie d'un signal réel à spectre continu, il faut normaliser la TFD par Pour mesurer une densité spectrale de puissance d'un signal réel à spectre continu, il faut normaliser la TFD par |
Application de la TFD au filtrage
On utilise la propriété
![]()
pour réaliser un filtrage à réponse impulsionnelle finie (RIF).
On calcule ![]()
La convolution nécessite ainsi le calcul de 3 TFD. En raison de l'existence d'un algorithme de calcul rapide de la TFD, cela est plus rapide que la convolution directe dès que N devient un peu grand (de l'ordre de 256).
Cependant cette opération réalise une convolution circulaire, qui n'est pas souhaitable pour faire un filtrage. Pour s'affranchir de cette difficulté, il suffit de prendre une taille de la TFD au moins aussi grande que celle du résultat de la convolution : si le signal possède ![]() points, et la réponse impulsionnelle
points, et la réponse impulsionnelle ![]() points, on calculera la TFD sur une longueur au moins égale à
points, on calculera la TFD sur une longueur au moins égale à ![]() . En pratique, on arrondira généralement à la puissance de 2 supérieure, car la plupart des algorithmes de calcul rapide de le TFD imposent que la longueur soit une puissance de 2. Pour obtenir cette longueur, on complète le signal ainsi que la réponse impulsionnelle par des zéros.
. En pratique, on arrondira généralement à la puissance de 2 supérieure, car la plupart des algorithmes de calcul rapide de le TFD imposent que la longueur soit une puissance de 2. Pour obtenir cette longueur, on complète le signal ainsi que la réponse impulsionnelle par des zéros.
On découpe le signal en blocs (ou "segments"). Si l'on effectue indépendamment la convolution (par TFD) des blocs par la réponse impulsionnelle désirée, on obtient des défauts importants. En effet, la continuité entre blocs n'est pas prise en compte et, en plus, la convolution réalisée est circulaire.
.
On filtre chaque bloc comme un signal à durée finie, en prenant la précaution de le prolonger par des zéros, comme indiqué ci-dessus. On obtient des réponses partielles qui se chevauchent. Il suffit de les sommer pour reconstituer le signal complet.
On utilise des blocs qui se chevauchent. On effectue la convolution sans précaution, donc circulaire. On ne garde que la partie des résultats non affectés par la circularité, et on les juxtapose.
Mesure ou compensation de retard par TFD
Soit un signal continu
![]()
Soit le signal continu retardé![]()
On sait que
![]()
On a vu que la TFD ![]() du signal échantillonné
du signal échantillonné ![]() est l'échantillonné de
est l'échantillonné de ![]() :
:
![]()
Donc
![]()
![]() avec
avec ![]()
Cette relation ressemble à celle donnée dans les propriétés de la TFD, mais ici, le retard peut être non entier.
On peut utiliser la relation précédente pour calculer les échantillons d'un signal retardé à partir des échantillons d'un signal, sans repasser par le signal continu. Il faut noter que l'opération réalisée est en fait un retard circulaire. Il convient donc de ne l'utiliser qu'avec des retards faibles devant la taille de la TFD. Cette opération est en fait un filtrage particulier, de type RIF, mais défini en fréquence. Voir le paragraphe précédent pour l'utilisation sur des signaux longs.
Soit
![]()
On cherche à mesurer le retard ![]() à partir de
à partir de ![]() et de
et de ![]()
Il suffit de calculer, par TFD, l'interspectre de ces deux signaux :
![]()
La phase de ![]() suit donc une loi linéaire, dont la pente donne le retard. En général, on utilisera cette méthode sur une portion finie de signaux infinis. Il faudra prendre garde à se placer dans des conditions où le retard est faible, et cela pour deux raisons.
suit donc une loi linéaire, dont la pente donne le retard. En général, on utilisera cette méthode sur une portion finie de signaux infinis. Il faudra prendre garde à se placer dans des conditions où le retard est faible, et cela pour deux raisons.
La première est, comme précédemment, la circularité du retard supposé par la méthode.
La seconde est que la phase est mesurée modulo ![]() . Et comme, en plus, elle est échantillonnée, il n'est plus possible de constater la linéarité dès que la pente est trop forte.
. Et comme, en plus, elle est échantillonnée, il n'est plus possible de constater la linéarité dès que la pente est trop forte.